image from livescience.com
In physics, is the concept that the mass of an object or system is a measure of its energy content. For instance, adding 25 kilowatt-hours(90 megajoules) of any form of energy to any object increases its mass by 1 microgram (and, accordingly, its inertia and weight) even though no matter has been added.
A physical system has a property called energy and a corresponding property called mass; the two properties are equivalent in that they are always both present in the same (i.e. constant) proportion to one another. Mass–energy equivalence arose originally from special relativity as a paradox described by Henri Poincaré.[1] The equivalence of energy E and mass m is reliant on the speed of light c and is described by the famous equation:
Thus, this mass–energy relation states that the universal proportionality factor between equivalent amounts of energy and mass is equal to the speed of light squared. This also serves to convert units of mass to units of energy, no matter what system of measurement units used.
If a body is stationary, it still has some internal or intrinsic energy, called its rest energy. Rest mass and rest energy are equivalent and remain proportional to one another. When the body is in motion (relative to an observer), its total energy is greater than its rest energy. The rest mass (or rest energy) remains an important quantity in this case because it remains the same regardless of this motion, even for the extreme speeds or gravity considered in special and general relativity; thus it is also called theinvariant mass.
On the one hand, the equation E = mc2 can be applied to rest mass (m or m0) and rest energy (E0) to show their proportionality as E0 = m0c2.[2]
On the other hand, it can also be applied to the total energy (Etot or simply E) and total mass of a moving body. The total mass is also called the relativistic mass mrel. The total energy and total mass are related by E = mc2.[3]
Thus, the mass–energy relation E = mc2 can be used to relate the rest energy to the rest mass, or to relate the total energy to the total mass. To instead relate the totalenergy or mass to the rest energy or mass, a generalization of the mass–energy relation is required: the energy–momentum relation.
E = mc2 has frequently been invoked as an explanation for the origin of energy in nuclear processes specifically, but such processes can be understood as converting nuclear potential energy in a manner precisely analogous to the way that chemical processes convert electrical potential energy. The more common association of mass–energy equivalence with nuclear processes derives from the fact that the large amounts of energy released in such reactions may exhibit enough mass that the mass loss (which is called the mass defect) may be measured, when the released energy (and its mass) have been removed from the system; while the energy released in chemical processes is smaller by roughly six orders of magnitude, and so the resulting mass defect is much more difficult to measure. For example, the loss of mass to an atom and a neutron, as a result of the capture of the neutron and the production of a gamma ray, has been used to test mass–energy equivalence to high precision, as the energy of the gamma ray may be compared with the mass defect after capture. In 2005, these were found to agree to 0.0004%, the most precise test of the equivalence of mass and energy to date. This test was performed in the World Year of Physics 2005, a centennial celebration of Albert Einstein's achievements in 1905.[4]
Einstein was not the first to propose a mass–energy relationship (see the History section). However, Einstein was the first scientist to propose the E = mc2 formula and the first to interpret mass–energy equivalence as a fundamental principle that follows from the relativistic symmetries of space and time.
this formula can also explain about how much energy would be released if a unit mass of matter and antimatter collides

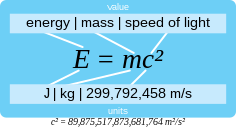
info via:wikipedia

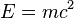
No comments:
Post a Comment